【julia】正規性の検定

検定を行う前に、データが正規性を持つか（正規分布しているといえるか）を検証する必要があります。検証方法としては、コルモゴロフ・スミルノフ検定 (Kolmogorov-Smirnov test)やシャピロ・ウィルク検定 (Shapiro-Wilk test)、アンダーソン・ダーリング検定（Anderson-Darling test)があります。

コルモゴロフ・スミルノフ検定

コルモゴロフ・スミルノフ検定は得られた2つのデータ間の確率分布の相違の検定、または、1データにおける確率分布の正規性を行う検定。１データで正規分布に従うとみなせるか否かを有意水準5%にて検定してみます。帰無仮説 (H₀) は標本分布が正規分布に従うことです。

まずは、パッケージの準備です。以下のパッケージを入れます。

julia:
using Pkg
Pkg.add(“HypothesisTests”)
Pkg.add(“Distributions”)
Pkg.add(“Plots”)

続いて、下記を実行します。Normal()はDistributionsパッケージで用意されエイル関数です。
まず、正規分布に従う300個のデータを乱数で発生させます。発生させたデータが、その平均と標準偏差が同じ正規分布と同じかどうかKSTestにて検定します。

using HypothesisTests
using Distributions
using Plots

dat = rand(Normal(),300)
mu = mean(dat)
sd = std(dat)
histogram(dat, bins=10)

println(ExactOneSampleKSTest(dat, Normal(mu, sd)))

発生させたデータをヒストグラムで確認します。

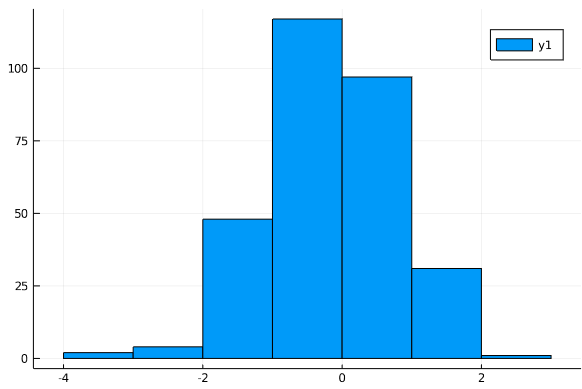
検定結果は、次の通り、帰無仮説を棄却できませんでしたので、正規分布となります（当然ですが）。

Exact one sample Kolmogorov-Smirnov test
----------------------------------------
Population details:
    parameter of interest:   Supremum of CDF differences
    value under h_0:         0.0
    point estimate:          0.05194102792297883

Test summary:
    outcome with 95% confidence: fail to reject h_0
    two-sided p-value:           0.3802

Details:
    number of observations:   300

こちらのサイトを参考にさせていただきました。