【R】独立性の検定
マーケティング等で得られたデータの有意差検定を行うことがあります。クロス集計表から各項目に関連がない(独立)かどうかを確認するものです(Chi-square test of independence)。ここでは、例として統計検定2級2013年11月の問15を検討してみます。
ある病院で好きな酒の種類とアルコール依存症の関係を調べるため、分割表を次のように作成しました。この表について検討します。
| 依存症である | 依存症でない | |
| ビール | 86 | 13 |
| 日本酒 | 32 | 42 |
| 焼酎 | 92 | 105 |
| ウイスキー | 24 | 31 |
| ワイン | 22 | 43 |
まずは、モザイクプロットで眺めてみます。
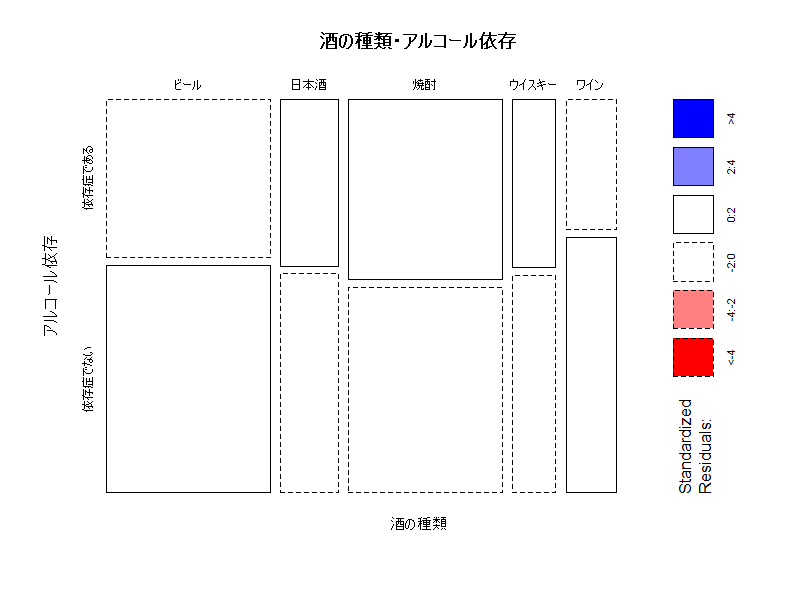
カテゴリカルデータの視覚化に多用されるようです。各グループの割合が面積で表示され、一目で全体を眺められて便利です。また、残差によって色分けされ、有意に多いグループが青色、有意に少ないグループが赤色です。さらに、その大きさによって、おおむね5%で薄い色、0.01%で薄い色となるようです。
検討に使用したコードは次の通りです。カイ二乗検定を手動と関数の2種類で行ってみました。
# カイ二乗検定(独立性の検定)
# データの準備
dat<-c(86, 32, 92, 24, 22, 123, 42, 105, 31, 43)
DF<-as.data.frame(matrix(dat, 5, 2, byrow=F))
colnames(DF)<-c("依存症である", "依存症でない")
rownames(DF)<-c("ビール", "日本酒", "焼酎", "ウイスキー", "ワイン")
# モザイクプロットで眺めてみる
mosaicplot(DF, xlab="酒の種類", ylab="アルコール依存", shade=TRUE, main="酒の種類・アルコール依存")
# 手動でカイ二乗検定
# 各行の合計を求める
r_sum<-c()
for (i in row(DF)){
r_sum[i]<-sum(DF[i,])
}
# 各列の合計を求める
c_sum<-c()
for (j in col(DF)){
c_sum[j]<-sum(DF[,j])
}
# 全合計
t_sum<-sum(c_sum)
# 期待値を計算
E_DF<-data.frame()
for (i in row(DF)){
for (j in col(DF)){
E_DF[i, j]<-r_sum[i] * c_sum[j] / t_sum
}
}
# 検定統計量Tの計算
T<-sum((DF-E_DF)*(DF-E_DF)/E_DF)
# 自由度4(=(5-1)×(2-1)), 有意水準5%のカイ二乗値を求める。
qchisq(0.95, 4)
# Rの関数を使って計算
chisq.test(DF)
検定統計量\(\chi^2\)は分割表の\(i\)行\(j\)列の観測度数\(O_{i,j}\)と期待度数\(E_{i,j}\)から次式で求めます。
$$\chi^2={\displaystyle \Sigma_{i,j}^{n}}\frac{(O_{i,j}-E_{i,j})^2}{E_{i,j}}$$
ここで、期待度数は、
$$E_{i,j}=\frac{n_{i}m_{j}}{N}$$
\(n_{i}=\Sigma_{j} O_{i,j}\), \(m_{j}=\Sigma_{i} O_{i,j}\), \(N=\Sigma_{i}n_{i} = \Sigma_{j}m_{j}\)
で計算されます。
手動で検定統計量T(\(=\chi^2\))を求めた結果、3.606となりました。自由度4、有意水準5%のカイ二乗値を求めると9.488で、帰無仮説を棄却できず、酒の種類とアルコール依存症は、独立ではないとはいえない(関連があるとはいえない)ことになります。
同じことをRの\(chiqs.test()\)でも行ってみました。
R:
Pearson's Chi-squared test data: DF X-squared = 3.6059, df = 4, p-value = 0.462
と同じ結果が得られました。

