【R】主成分分析とクラスタリング
1.はじめに
主成分分析(principal component analysis)は、多変量解析の一つで、多変量データの情報をなるべく削らずに、少数の変数に次元を下げる手法です。
Rで主成分分析を行う関数は、princompかprcompで、princomp関数は固有値と固有ベクトルの計算に基づき、prcomp関数は特異値分解の戻づくらしいです。このうち、prcompが優れているらしいので、こちらを使います。
2.データ
総務省統計局が発表している「都道府県・市区町村のすがた(社会・人口統計体系)」から、各都道府県の産業構成と県民所得を元に都道府県を分類してみます。
具体的には、2014年の以下のデータを取得します。ただしm付加価値額だけは、2015年のデータです。
・C1115_県内総生産額(第1次産業)(平成23年基準)【百万円】
・C1116_県内総生産額(第2次産業)(平成23年基準)【百万円】
・C1117_県内総生産額(第3次産業)(平成23年基準)【百万円】
・C120101_1人当たり県民所得(平成17年基準)【千円】
・C2110_第1次産業事業所数(経済センサス‐基礎調査結果)【所】
・C2111_第2次産業事業所数(経済センサス‐基礎調査結果)【所】
・C2112_第3次産業事業所数(経済センサス‐基礎調査結果)【所】
・C6201_付加価値額(民営)【百万円】
・C6301_売上高(サービス産業)【百万円】
データは、まとめて「prcomp_pref_dat.csv」ファイルに保存しました。
3.主成分分析
Rのコードは次の通りです。
library(ggplot2)
library(ggrepel)
dat<-read.csv("http://www.dinov.tokyo/Data/JP_Pref/prcomp_pref_dat.csv", header = TRUE, fileEncoding="UTF-8")
rownames(dat)<-dat$地域
head(dat)
ret<-prcomp(dat[,c(-1)], scale=TRUE )
print(ret)
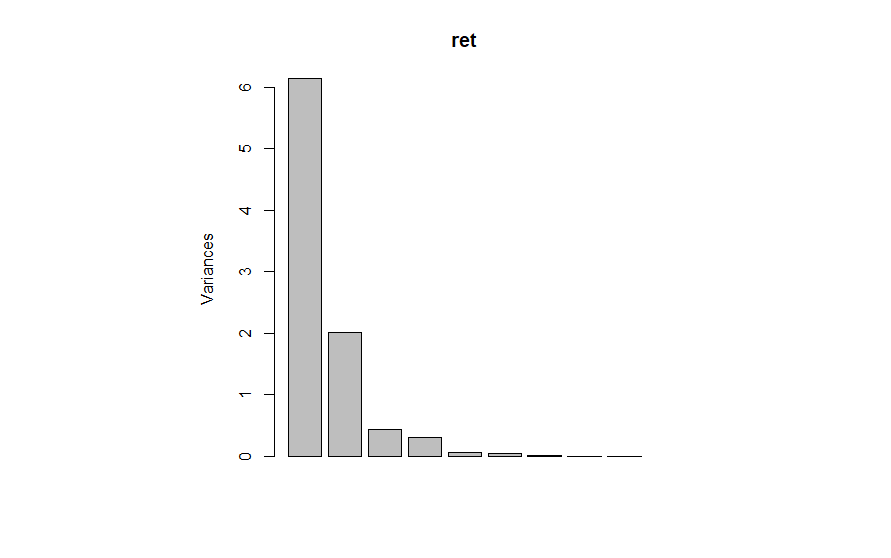
screeplot(ret)
biplot(ret)
スクリープロットの結果から、固有値が1より大きい第2主成分までが有効であるとわかる。
prcompの結果を見ると、次の通りです。
Standard deviations (1, .., p=9):
[1] 2.47732120 1.41988548 0.65727103 0.55241447 0.24904064 0.19370418 0.09276941 0.03241589 0.02093905
Rotation (n x k) = (9 x 9):
PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8
県内総生産額_1次 -0.01764482 0.693911426 -0.09046023 0.09077635 -0.3184161 0.631910347 -0.01400230 0.017366884
県内総生産額_2次 -0.36656244 -0.005073508 -0.42794338 -0.48524799 -0.5848253 -0.286662260 -0.05958400 -0.127170062
県内総生産額_3次 -0.38976656 -0.012779828 0.32729276 0.25134094 -0.1293618 -0.055357079 0.13906998 -0.539442917
県民所得 -0.31913293 -0.175190116 -0.70110140 0.56623195 0.1996979 0.100065511 -0.07182487 0.009934825
事業所数_1次 -0.03413400 0.691919974 -0.07623580 0.12241415 0.2833180 -0.643885478 0.05768995 -0.003910638
事業所数_2次 -0.38194918 0.050672487 -0.09298219 -0.48936144 0.5363062 0.272500083 0.49028592 -0.033677867
事業所数_3次 -0.39391953 0.070447984 0.19373101 -0.18290325 0.2873822 0.090997262 -0.82267921 0.033808688
付加価値額 -0.39738348 -0.025246031 0.22129207 0.12749670 -0.1878329 -0.091048017 0.17163160 0.811396368
売上高_サービス産業 -0.38912762 -0.026173653 0.33023964 0.26140832 -0.1192209 0.004637022 0.14760590 -0.178247636
PC9
県内総生産額_1次 -0.023558753
県内総生産額_2次 0.055558470
県内総生産額_3次 -0.589481022
県民所得 -0.012286178
事業所数_1次 0.032916292
事業所数_2次 -0.005626223
事業所数_3次 -0.008124851
付加価値額 -0.211733366
売上高_サービス産業 0.776342223biplotで結果を表示すると次の通りです。
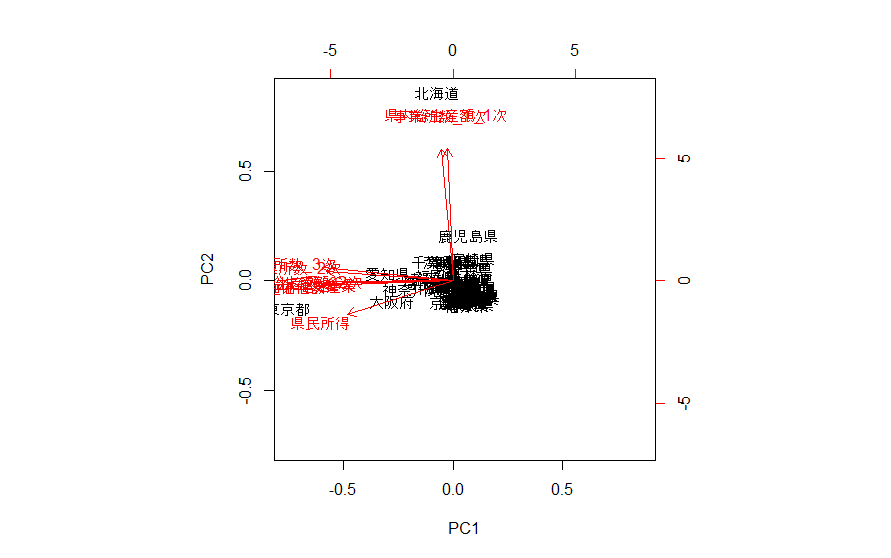
この結果から、
・第1次産業関連は、他の項目と比べて遠い関係にある。
・第1次産業関連以外は、かなり近い関係にあるが、県民所得だけ少し外れている。
・北海道と東京が突出している。
がわかります。
4.クラスタリング
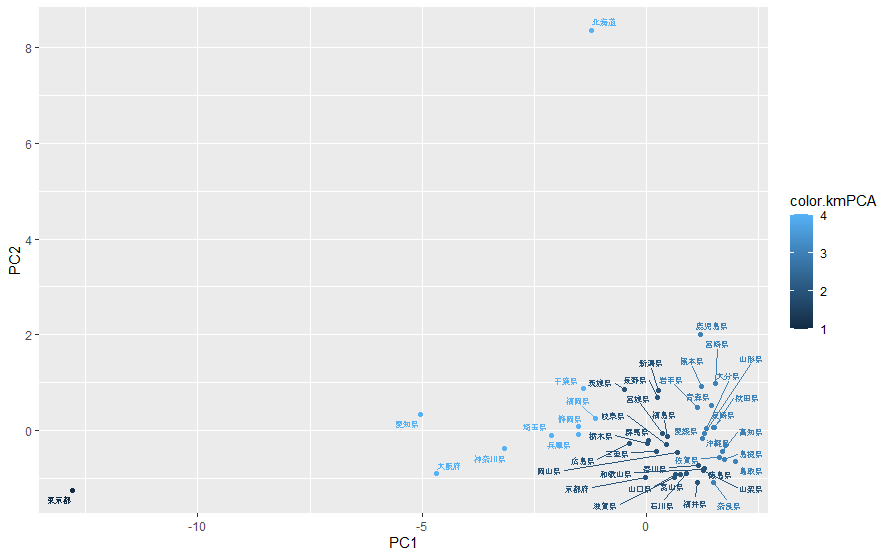
k平均法を用いて、主成分得点によるクラスタリングを行い、その摘果をプロットします。
DFpca<-as.data.frame(reet$x) rownames(DFpca)<-dat$地域 kmPCA<-kmeans(DFpca[,1:3], 4, iter.max=50) color.kmPCA<-kmPCA$cluster ggplot(data=DFpca) + geom_point(aes(x=PC1, y=PC2, col=color.kmPCA)) + geom_text_repel(aes(x = PC1, y = PC2, label = rownames(DFpca), col=color.kmPCA), family = "serif", size = 2)