【R】クラスタリング
1.はじめに
解釈をわかりやすくしたり、2次的に利用するために、ある集団をグループに分ける(分類する)ことが良くあります。この分類には、大きく2つの考え方があります。
(1)分類:各個体が持つ特徴を総合的に考慮して、似た者同士を複数のグループに分けること。
(2)判別・識別:各個体の特徴から、どの種類のグループに属するかを判別すること。
(1)は機械学習でいうところの「教師なし学習」で、(2)は「教師あり学習」となります。ここでは、一般的にクラスタリング(クラスター分析)と言われる(1)の「分類」を行ってみます。
クラスタリングには、階層的クラスタリングと非階層的クラスタリング、そしてモデルベースクラスタリングがあります。
階層型クラスタリングは、似た者同士をまとめていく手法です。初期状態として、あるクラスターを仮定し(各クラスターに個体が一つでもよい)、クラスター間の距離を計算する。距離の近いクラスターを併合して1つのクラスターとする。ある作成手順に従いクラスターを併合していき、クラスター数が1になるまで繰り返す。最終的には、樹形図(Dendrogram)にて表示し、どのクラスターにするか分析者が判断します。クラスターを作っていくイメージは、この樹形図の下から上に上がっている様子と同じです。
距離の計算方法は、ユークリッド距離、マンハッタン距離、最長距離、ミンコフスキー距離、キャンベラ距離、バイナリー距離等があるようです。また、クラスター作成方法は、ウォード法、最短距離法、最長距離法、McQuitty法、メディアン法、重心法、軍平均法があるようです。ここでは、最も明確なクラスターを作成できるウォード法を使用します。このとき、ユークリッド平方距離を使うと良いそうです。
非階層型クラスタリングの代表的な手法であるk-means法は、階層型クラスタリングとは異なり、階層的な構造を持たず、あらかじめクラスターの数kを決め、その数kに近い点から順にクラスターをまとめていきます。一度、クラスターができると、中心点が各クラスタの重心に移動して、再度クラスターを構成します。これを繰り返し最終的なクラスターに分類する手法です。
一般に、個体数が大きいビッグデータの分析に適しているようです。
ただし、あらかじめいくつのクラスターに分けるかは、分析者が決める必要があります。また、最初の点により最終的なクラスターが異なります。したがって、分析ごとに結果が異なります。
モデルベースクラスタリングは、外部から観察できない潜在変数を推定してクラスタリングを行う方法です。このような変数の推定は最尤推定を用いるのが一般的ですが、複数の正規分布がある割合で混ざった混合正規分布は、確率分布もわからなければ、潜在変数もわかりません。この場合は、EMアルゴリズムを用います。
この方法は、EステップとMステップからなり、Eステップで確率分布のパラメータから潜在変数を推定します。次のMステップで推定した潜在変数をもとに確率分布のパラメータw推定し、実測データを補完します。このようにモデルを推定するため、モデルベースクラスタリングと呼ばれています。繰り返しシミュレーションし最尤推定するため堅実なアルゴリズムですが、計算量が多く、時間がかかります。
2.データ
日本の都道府県を産業構造で分類してみたいと思います。総務省統計局が発表している「都道府県・市区町村のすがた(社会・人口統計体系)」からまとめたデータ http://www.dinov.tokyo/Data/JP_Pref/prcomp_pref_dat.csv のうち、以下の4項目を抜き出して使用します。
・県内総戦線額_1次
・県内総戦線額_2次
・県内総戦線額_3次
・付加価値額
#データ準備
dat<-read.csv("http://www.dinov.tokyo/Data/JP_Pref/prcomp_pref_dat.csv", header = TRUE, fileEncoding="UTF-8")
rownames(dat)<-dat$地域
dat_a<-dat[,c(2:4,9)] # 県内総戦線額_1次、_2次、_3次、付加価値額のみを使う
head(dat_a)
> head(dat_a)
県内総生産額_1次 県内総生産額_2次 県内総生産額_3次 付加価値額
北海道 751786 3103163 14355411 9217331
青森県 162939 1012574 3215849 1926570
岩手県 148298 1346577 3101874 2131413
宮城県 109833 2454796 6592177 5172146
秋田県 87874 755347 2514665 1637454
山形県 119599 1063816 2610010 18867863.クラスタリング
3.1 階層型クラスタリング
・dist()関数で距離を計算します。
・hclust()関数でクラスタリングします。
・plot()関数でデンドログラムを表示します。
# 階層型クラスタリング DIST<-dist(dat_a) result.hc<-hclust(DIST, method = "ward") plot(result.hc, hang=0.2)

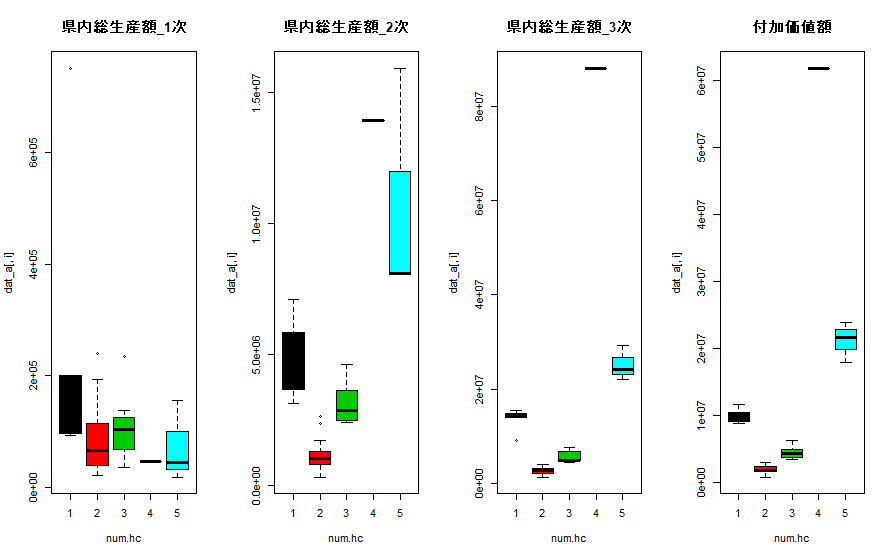
この結果から、都道府県を5つに分類するとよさそうです。今度は、結果を変数ごとにボックスプロットで表示してみます。
num.hc<-cutree(result.hc, k=5)
layout(matrix(1:4, 1, 4))
for (i in 1:4){
boxplot(dat_a[,i] ~ num.hc, main=colnames(dat_a)[i], col=c(1,2,3,4,5))
}
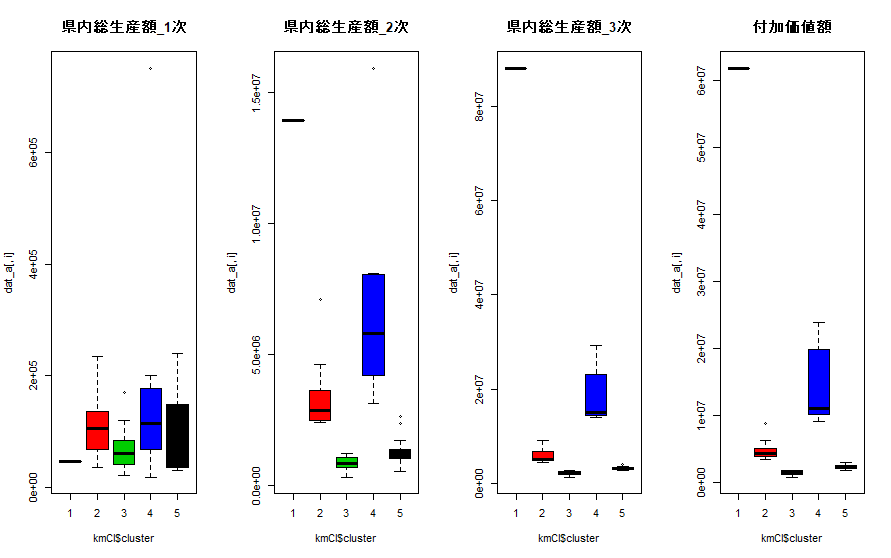
3.2 非階層型クラスタリング
・kmeans()関数で計算(3.1の結果を活かして5つのクラスターとする)
# 非階層型クラスタリング kmCl<-kmeans(dat_a, 5, iter.max=50)
結果を変数ごとにボックスプロットで表示してみます。
layout(matrix(1:4, 1, 4))
for (i in 1:4){
boxplot(dat_a[,i] ~ kmCl$cluster, main=colnames(dat_a)[i], col=c(1,2,3,4))
}
3.3 両者の比較
階層型クラスタリングと非階層型クラスタリングの2つの方法でクラスタリングしてみました。その結果を、日本地図で表して比較してみましょう。
library(NipponMap)
#地図にプロットして比較
windowsFonts(JP4=windowsFont("Biz Gothic"))
windows(width=1600, height=800)
par(family="JP4")
layout(matrix(1:2, 1, 2))
JapanPrefMap(num.hc, main="階層型クラスタリング結果") # 階層型クラスタリング結果
JapanPrefMap(kmCl$cluster, main="非階層型クラスタリング結果") # 非階層型クラスタリング結果
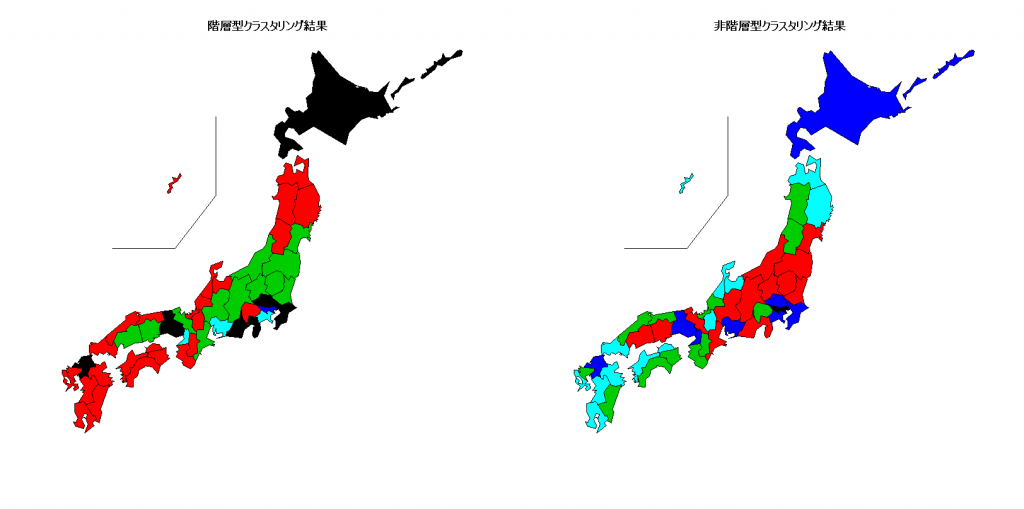
両者は、似たような結果ですが、多少異なっていますね。あとは、分析者の判断となります。
3.4 モデルベースクラスタリング
最後にモデルベースクラスタリングを簡単に見てみます。パッケージmclustを用います。そして、Mclust関数でモデルベースクラスタリングを実行します。
library(mclust) dat.mclust <- Mclust(dat_a) summary(dat.mclust)
----------------------------------------------------
Gaussian finite mixture model fitted by EM algorithm
----------------------------------------------------
Mclust VEE (ellipsoidal, equal shape and orientation) model with 5 components:
log-likelihood n df BIC ICL
-2712.187 47 38 -5570.68 -5571.277
Clustering table:
1 2 3 4 5
4 5 13 18 7 注目するのは、BIC(ベイズ情報量基準)です。これが小さい時に確からしいモデルとなります。Mclust関数では、さまざまな確率分布をシミュレーションして最も小さいBIC値を最適クラスター数として採用します。
dat.mclust$BICこのコマンドで各種の確率分布におけるBIC値を確認できます。
Bayesian Information Criterion (BIC):
EII VII EEI VEI EVI VVI EEE EVE VEE VVE EEV
1 -6546.606 -6546.606 -6116.822 -6116.822 -6116.822 -6116.822 -5800.556 -5800.556 -5800.556 -5800.556 -5800.556
2 -6318.984 -6074.146 -6023.895 -5810.055 -5956.831 -5798.106 -5756.326 NA -5612.078 -5626.960 -5674.453
3 -6133.569 -5968.910 -5994.786 -5762.694 -5892.922 -5738.579 -5766.842 NA -5590.835 -5595.310 -5646.916
4 -6152.819 -5874.275 -6014.034 -5747.782 -5841.196 -5745.877 -5785.781 NA -5595.476 -5607.598 -5669.573
5 -5935.108 -5877.985 -6033.311 -5675.246 -5851.610 -5688.866 -5795.087 NA -5570.680 NA -5707.558
6 -5954.359 NA -5972.431 NA NA NA -5722.275 NA NA NA -5746.248
7 -5944.766 NA -5735.275 NA NA NA -5665.385 NA NA NA -5665.068
8 -5879.572 NA -5686.680 NA NA NA -5621.471 NA NA NA -5636.229
9 -5890.749 NA -5681.119 NA NA NA -5610.961 NA NA NA -5676.011
VEV EVV VVV
1 -5800.556 -5800.556 -5800.556
2 -5611.613 NA -5594.498
3 -5611.762 NA NA
4 -5603.732 NA NA
5 -5619.474 NA -5644.589
6 NA NA NA
7 NA NA NA
8 NA NA NA
9 NA NA NA
Top 3 models based on the BIC criterion:
VEE,5 VEE,3 VVV,2
-5570.680 -5590.835 -5594.498 表示が崩れて見にくいのですが。。。EII~VVVがモデルの種類です。これらのモデルの中で絶対値が最も小さいVEEのクラスター数5が最適クラスター数となります。
グラフにて確認するときは、
plot(dat.mclust)コマンドで、表示されるメニューから、1.BICを選択します。
> plot(dat.mclust)
Model-based clustering plots:
1: BIC
2: classification
3: uncertainty
4: densityすると、次のようなプロットが表示されます。
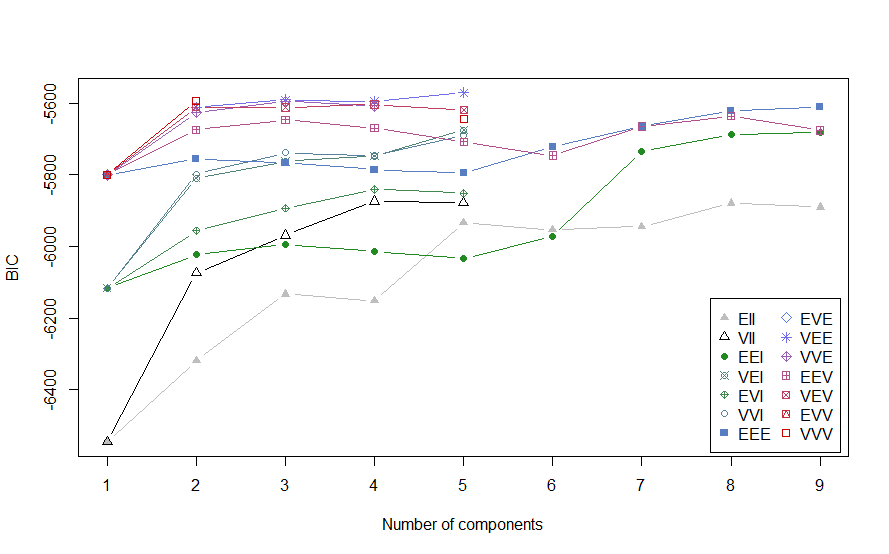
このプロットからも、モデルVEEでクラスター数5がBICの絶対値が最も小さいことが分かります。
4.さいごに
データさえそろってしまえば、処理は簡単であることがわかりました。どういう解釈をするかが、難しいですね。

