【R】Rとstanでベイズ推定
1.はじめに
内閣府のページに、年齢別身長・体重・座高の全国平均値が掲載されています。このうち、6~17歳男子の身長のモデルをマルコフ連鎖モンテカルロ法(MCMC)を利用したベイズ推定してみます。
MCMCを利用したベイズ推定のソフトウエアは、WinBUGSとJAGSが有名らしいのですが、どちらも使いにくかったり開発が停滞しているらしいです。ここでは、現在もっとも開発が活発なStanを使用します。
Stanの事後分布の推定アルゴリズムはハミルトンモンテカルロの一つであるNUTS(No-U-Turn Sampler)です。これは、パラメータが多い場合にも効率よくサンプリングが可能で、開発が活発なこともあり広く利用されています。Rからはrstanというパッケージを利用します。
2.準備
まず、Rtoolsをインストールします。使用しているRのバージョンに遭ったRtoolsをセレクトします。インストールの途中でPATHの指定がある場合には、指定するようにチェックします。もしくは、インストール後にRから、次のコマンドを入力します。
writeLines('PATH="${RTOOLS40_HOME}\\usr\\bin;${PATH}"', con = "~/.Renviron")続いて、rstanをCRANからインストールします。
install.packages("rstan")
library(rstan)3.ベイズ推定してみる
3.1 データ
データを読み込みます。成形してある年齢(X)、身長(Y)データを読み込みます。
dat <- read.csv("http://www.dinov.tokyo/Data/JP_Pref/height.csv", header = TRUE, fileEncoding="UTF-8")
standata<-list(N=nrow(dat), X=dat$X, Y=dat$Y)
3.2 stanコードの記述
stanコードはブロックに分かれて記述します。ここでは、全てRのファイル内で記述しますが、このコード部を別ファイルとして呼び出すこともできます。
線形回帰の各パラメータが正規分布するとして推定してみます。
Model_w="
data {
int N;
real X[N];
real Y[N];
}
parameters {
real a;
real b;
real<lower=0> sigma;
}
model {
for (i in 1:N)
Y[i] ~ normal(a + b*X[i], sigma); // 正規分布をもとにa,bを推定
}
"
3.3 stanでパラメータ推定(mcmc実行)
Model1.1=stan(model_code=Model_w,data=standata,iter=1000,thin=1,chains=4)
AMPLING FOR MODEL 'd353dcd293e284b68aec83b3ba300104' NOW (CHAIN 1).
Chain 1:
Chain 1: Gradient evaluation took 0 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1:
Chain 1:
Chain 1: Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 1: Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 1: Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 1: Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 1: Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 1: Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 1: Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 1: Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 1: Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 1: Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 1: Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 1: Iteration: 1000 / 1000 [100%] (Sampling)
Chain 1:
Chain 1: Elapsed Time: 0.071 seconds (Warm-up)
Chain 1: 0.063 seconds (Sampling)
Chain 1: 0.134 seconds (Total)
Chain 1:
SAMPLING FOR MODEL 'd353dcd293e284b68aec83b3ba300104' NOW (CHAIN 2).
Chain 2:
Chain 2: Gradient evaluation took 0 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2:
Chain 2:
Chain 2: Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 2: Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 2: Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 2: Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 2: Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 2: Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 2: Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 2: Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 2: Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 2: Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 2: Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 2: Iteration: 1000 / 1000 [100%] (Sampling)
Chain 2:
Chain 2: Elapsed Time: 0.086 seconds (Warm-up)
Chain 2: 0.061 seconds (Sampling)
Chain 2: 0.147 seconds (Total)
Chain 2:
SAMPLING FOR MODEL 'd353dcd293e284b68aec83b3ba300104' NOW (CHAIN 3).
Chain 3:
Chain 3: Gradient evaluation took 0 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3:
Chain 3:
Chain 3: Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 3: Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 3: Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 3: Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 3: Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 3: Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 3: Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 3: Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 3: Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 3: Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 3: Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 3: Iteration: 1000 / 1000 [100%] (Sampling)
Chain 3:
Chain 3: Elapsed Time: 0.062 seconds (Warm-up)
Chain 3: 0.06 seconds (Sampling)
Chain 3: 0.122 seconds (Total)
Chain 3:
SAMPLING FOR MODEL 'd353dcd293e284b68aec83b3ba300104' NOW (CHAIN 4).
Chain 4:
Chain 4: Gradient evaluation took 0 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4:
Chain 4:
Chain 4: Iteration: 1 / 1000 [ 0%] (Warmup)
Chain 4: Iteration: 100 / 1000 [ 10%] (Warmup)
Chain 4: Iteration: 200 / 1000 [ 20%] (Warmup)
Chain 4: Iteration: 300 / 1000 [ 30%] (Warmup)
Chain 4: Iteration: 400 / 1000 [ 40%] (Warmup)
Chain 4: Iteration: 500 / 1000 [ 50%] (Warmup)
Chain 4: Iteration: 501 / 1000 [ 50%] (Sampling)
Chain 4: Iteration: 600 / 1000 [ 60%] (Sampling)
Chain 4: Iteration: 700 / 1000 [ 70%] (Sampling)
Chain 4: Iteration: 800 / 1000 [ 80%] (Sampling)
Chain 4: Iteration: 900 / 1000 [ 90%] (Sampling)
Chain 4: Iteration: 1000 / 1000 [100%] (Sampling)
Chain 4:
Chain 4: Elapsed Time: 0.077 seconds (Warm-up)
Chain 4: 0.077 seconds (Sampling)
Chain 4: 0.154 seconds (Total)
Chain 4: 3.4 結果の確認
結果を見てみます。
Model1.1
> Model1.1
Inference for Stan model: d353dcd293e284b68aec83b3ba300104.
4 chains, each with iter=1000; warmup=500; thin=1;
post-warmup draws per chain=500, total post-warmup draws=2000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
a 85.99 0.14 3.70 78.37 83.71 86.08 88.39 93.08 666 1.01
b 5.37 0.01 0.31 4.76 5.17 5.36 5.56 5.98 649 1.00
sigma 3.60 0.04 1.03 2.22 2.88 3.42 4.09 6.19 611 1.00
lp__ -19.32 0.07 1.43 -23.01 -19.99 -18.97 -18.30 -17.68 421 1.00
Samples were drawn using NUTS(diag_e) at Fri Jun 19 14:53:21 2020.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).収束判定指標Rhatが1.05以下ですので、うまく収束しています。結果をプロットしてみます。
plot(Model1.1)

stanの関数でもプロットできます。
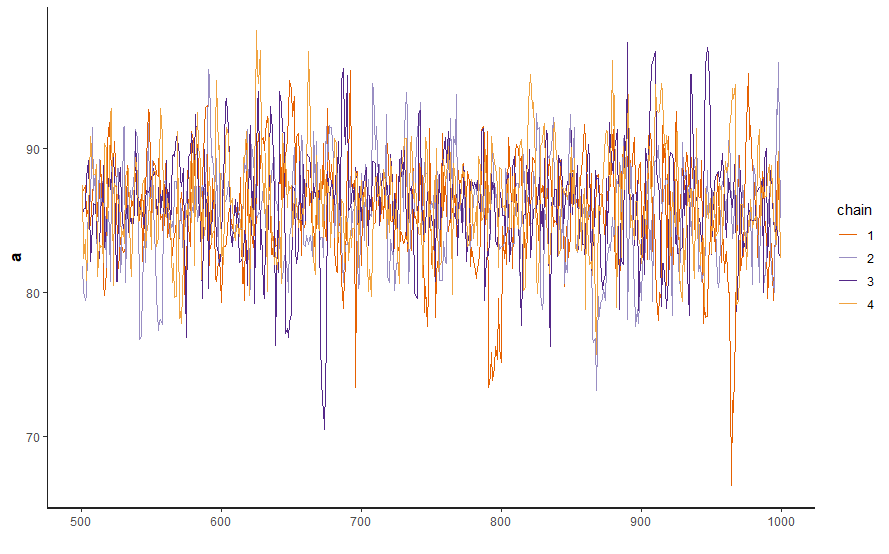
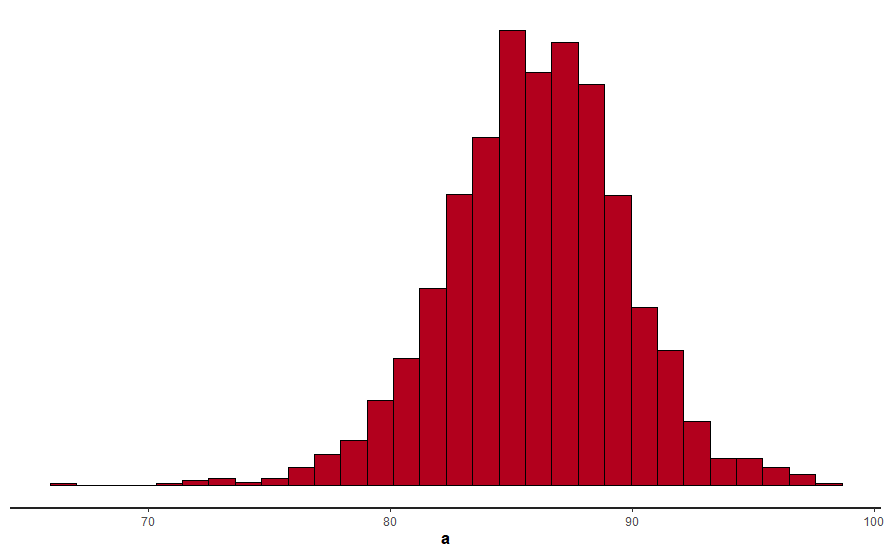
stan_trace(Model1.1, pars = "a") stan_hist(Model1.1, pars = "a") stan_dens(Model1.1, pars = "a", separate_chains = TRUE) stan_ac(Model1.1, pars = "a", separate_chains = TRUE)
Rからstanに値を渡してプロットする場合には、次のようにします。
a<-rstan::extract(Model1.1)$a hist(a)

codaパッケージを使って事後確率を見ることもできます。
require("coda")
d.fit.Model1.1<-mcmc.list(lapply(1:ncol(Model1.1),function(x) mcmc(as.array(Model1.1)[,x,])))
plot(d.fit.Model1.1)

また、ggmcmcにてPDFファイルに落とすこともできます。
library(ggmcmc) ggmcmc(ggs(Model1.1))
このようなggmcmc-outpu.pdfというPDFファイルができます。
3.5 モデルの保存と再利用
推定したモデルをファイルに保存しておき、後から利用することもできます。
saveRDS(Model2.1, "Model2.rds")
models_l <- readRDS("Model2.rds")
4. おわりに
ベイズ推定で、年齢から身長を求めるモデルのパラメータa,b,シグマの事後確率を求めてみました。