【R】modeltime

1. はじめに

tidymodelsパッケージを使えば、時系列データの予測も簡単にできます。modeltimeパッケージでは、古典的な時系列予測と機械学習を一度に扱えます。Getting Started with Modeltimeのページを参考に勉強してみます。

modeltimeのワークフローは次の通り。
＊学習用／テスト用データの準備
＊複数のモデルの生成とFit
＊FitしたモデルをModelTableに追加
＊モデルのキャリブレーション
＊テストデータでの予測と精度評価
＊Refitと予測

2. 使ってみる

2.1 準備

library(tidymodels)
library(modeltime)
library(tidyverse)
library(lubridate)
library(timetk)

interactive <- TRUE　#インタラクティブプロット

2.2 データ

データは、4th M competitionのデータセットを使います。詳細はこちら。データは、id毎に分けられており、m1, m2 ,m750, m1000がありますが、m750を使います。なぜなら、予測に使いやすいデータなので（笑）。

使用するm4_monthlyというデータはこんな感じ。

# A tibble: 1,574 x 3
   id    date       value
   <fct> <date>     <dbl>
 1 M1    1976-06-01  8000
 2 M1    1976-07-01  8350
 3 M1    1976-08-01  8570
 4 M1    1976-09-01  7700
 5 M1    1976-10-01  7080
 6 M1    1976-11-01  6520
 7 M1    1976-12-01  6070
 8 M1    1977-01-01  6650
 9 M1    1977-02-01  6830
10 M1    1977-03-01  5710
# ... with 1,564 more rows

このうち、idがm750のデータのみを使います。

m750 <- m4_monthly %>% filter(id == "M750")

プロットして確認します。

m750 %>%
  plot_time_series(date, value, .interactive = interactive)

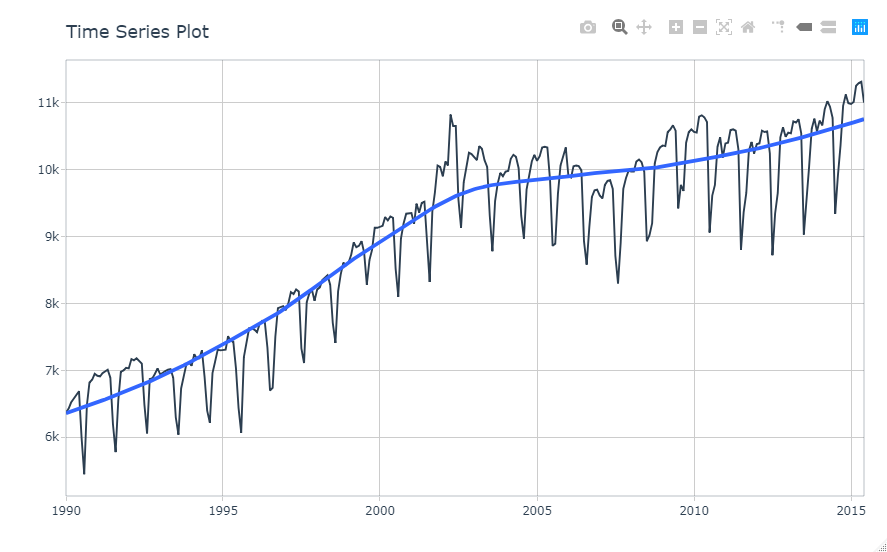
何となく、予測しやすそうなグラフ（笑）。

学習用とテスト用のデータに分けます。

splits <- initial_time_split(m750, prop = 0.9)

2.3 複数モデルの生成とFit

ここでは、モデルを６つ作ってみて、どれが良いかを比べてみます。modeltimeとparsnipを使ってモデルを作ります。

2.3.1 モデル１　Auto ARIMA (modeltime)

model_fit_arima_no_boost <- arima_reg() %>%
    set_engine(engine = "auto_arima") %>%
    fit(value ~ date, data = training(splits))

2.3.2 モデル２　Boosted Auto ARIMA(modeltime)

model_fit_arima_boosted <- arima_boost(
    min_n = 2,
    learn_rate = 0.015
) %>%
    set_engine(engine = "auto_arima_xgboost") %>%
    fit(value ~ date + as.numeric(date) + factor(month(date, label = TRUE), ordered = F),
        data = training(splits))

2.3.3 モデル３ Exponential Smoothing (modeltime)

model_fit_ets <- exp_smoothing() %>%
    set_engine(engine = "ets") %>%
    fit(value ~ date, data = training(splits))

2.3.4 モデル４ prophet (modeltime)

model_fit_prophet <- prophet_reg() %>%
    set_engine(engine = "prophet") %>%
    fit(value ~ date, data = training(splits))

2.3.5 モデル５　Linear Regression(parsnip)

model_fit_lm <- linear_reg() %>%
    set_engine("lm") %>%
    fit(value ~ as.numeric(date) + factor(month(date, label = TRUE), ordered = FALSE),
        data = training(splits))

2.3.6 モデル６　Multivariate Adaptive Regression Spline(MARS)(workflow)

model_spec_mars <- mars(mode = "regression") %>%
    set_engine("earth")

recipe_spec <- recipe(value ~ date, data = training(splits)) %>%
    step_date(date, features = "month", ordinal = FALSE) %>%
    step_mutate(date_num = as.numeric(date)) %>%
    step_normalize(date_num) %>%
    step_rm(date)

wflw_fit_mars <- workflow() %>%
    add_recipe(recipe_spec) %>%
    add_model(model_spec_mars) %>%
    fit(training(splits))

2.4 ModelTableへの追加

上記、6つのモデルをモデルテーブルへ追加します。

models_tbl <- modeltime_table(
    model_fit_arima_no_boost,
    model_fit_arima_boosted,
    model_fit_ets,
    model_fit_prophet,
    model_fit_lm,
    wflw_fit_mars
)

models_tbl

> models_tbl
# Modeltime Table
# A tibble: 6 x 3
  .model_id .model     .model_desc                              
      <int> <list>     <chr>                                    
1         1 <fit[+]>   ARIMA(1,0,1)(0,1,1)[12]                  
2         2 <fit[+]>   ARIMA(1,0,1)(0,1,1)[12] W/ XGBOOST ERRORS
3         3 <fit[+]>   ETS(A,N,A)                               
4         4 <fit[+]>   PROPHET                                  
5         5 <fit[+]>   LM                                       
6         6 <workflow> EARTH 

2.5 モデルのキャリブレーション

calibration_tbl <- models_tbl %>%
    modeltime_calibrate(new_data = testing(splits))

calibration_tbl

> calibration_tbl
# Modeltime Table
# A tibble: 6 x 5
  .model_id .model     .model_desc                               .type .calibration_data
      <int> <list>     <chr>                                     <chr> <list>           
1         1 <fit[+]>   ARIMA(1,0,1)(0,1,1)[12]                   Test  <tibble [31 x 4]>
2         2 <fit[+]>   ARIMA(1,0,1)(0,1,1)[12] W/ XGBOOST ERRORS Test  <tibble [31 x 4]>
3         3 <fit[+]>   ETS(A,N,A)                                Test  <tibble [31 x 4]>
4         4 <fit[+]>   PROPHET                                   Test  <tibble [31 x 4]>
5         5 <fit[+]>   LM                                        Test  <tibble [31 x 4]>
6         6 <workflow> EARTH                                     Test  <tibble [31 x 4]>

2.6 予測と精度評価

まずは、プロットして予測の精度を可視化してみます。

calibration_tbl %>%
    modeltime_forecast(
        new_data    = testing(splits),
        actual_data = m750
    ) %>%
    plot_modeltime_forecast(
      .legend_max_width = 25, 
      .interactive      = interactive
    )

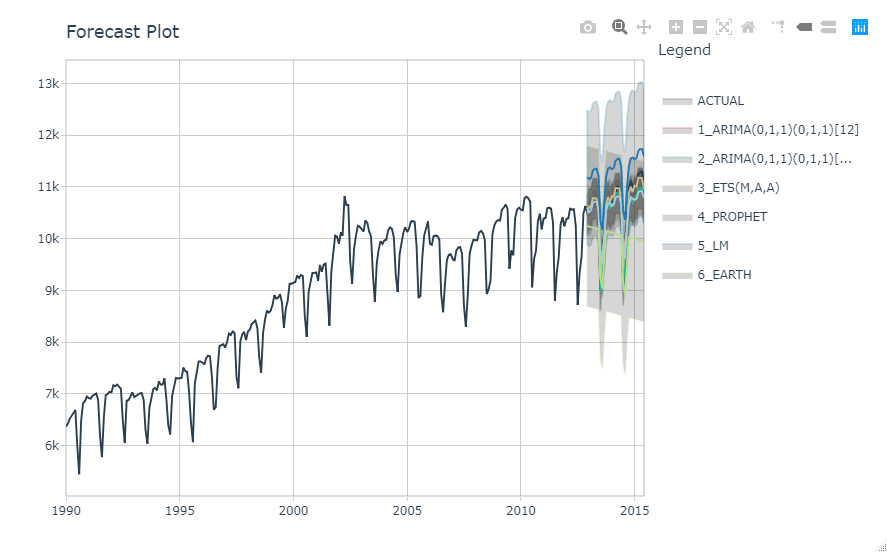
モデル３が最もよく、モデル１、２、４が同程度に良いです。モデル６はオーバーフィッティングです。数値でちゃんと確認してみます。

calibration_tbl %>%
    modeltime_accuracy() %>%
    table_modeltime_accuracy(resizable = TRUE, bordered = TRUE)

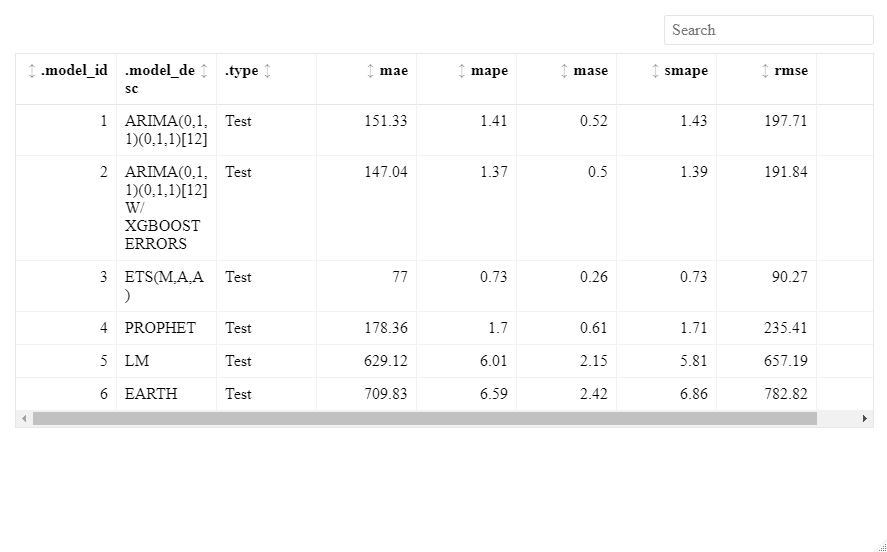
yardstickパッケージの評価結果を表示しています。
MAE-Mean Absolute Error,
MAPE-Mean Absolute Percentage Error,
MASE – Mean Absolute Square Error,
SMAPE – Symmetric Mean Absolute Percentage Error,
RMSE – Root Mean Squared Error,
RSQ – R – Squared

この結果からもモデル３が最も良いことが分かります。

2.7 Refitと将来予測

Refitをして、5年分の将来予測をしてみます。

refit_tbl <- calibration_tbl %>%
    modeltime_refit(data = m750)

refit_tbl %>%
    modeltime_forecast(h = "5 years", actual_data = m750) %>%
    plot_modeltime_forecast(
      .legend_max_width = 25, 
      .interactive      = interactive
    )

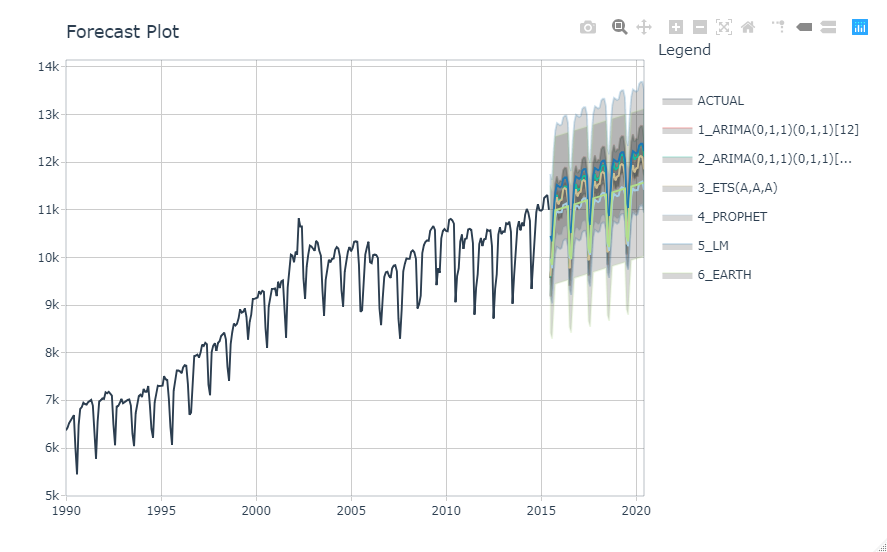
3. さいごに

色々なモデルを比較でき、最も良いモデルを探すことができました。これぐらい将来予測できると十分です。実際のビジネスでも使えるようになりたいですね。