【julia】統計解析(線形回帰)
2020年4月8日
RDatasetsのISLRからAutoのデータを読み込み、いろいろグラフをプロットしてみてから、HorsepowerとAccelerationの関係を線形回帰してみます。
using RDatasets, Gadfly, DataFrames, DataFramesMeta, Statistics, HypothesisTests,
Fontconfig, Cairo, GLM, Distributions, Distances, LinearAlgebra
set_default_plot_size(30cm, 8cm)
# データ読込
#RDatasets.packages()
RDatasets.datasets("ISLR")
dat = RDatasets.dataset("ISLR","Auto")
# いろいろプロットしてみる
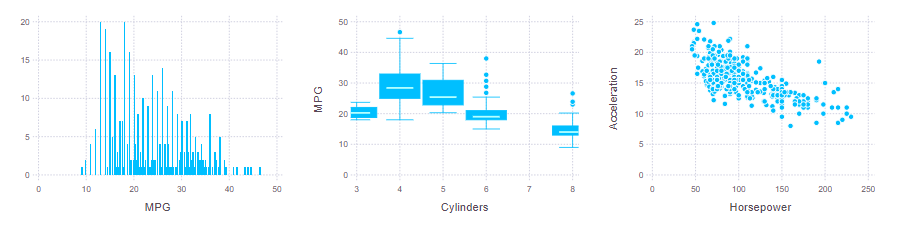
hstack(Gadfly.plot(dat, x = :MPG, Geom.histogram()),
Gadfly.plot(dat, x = :Cylinders, y = :MPG, Geom.boxplot),
Gadfly.plot(dat, x = :Horsepower, y = :Acceleration, Geom.point) )
# 線形回帰して、モデルの値(期待値)を計算し、診断プロットを描く
model = lm(@formula(Acceleration ~ Horsepower), dat)
pred = predict(model)
set_default_plot_size(16cm, 16cm)
Gadfly.plot(layer(x=dat[:Horsepower], y=dat[:Acceleration], Geom.point, Theme(default_color=color("red"))),
layer(x=dat[:Horsepower], y=pred, Geom.line, Theme(default_color=color("blue"))), Guide.title("Horsepower vs Acceleration"),
Guide.xlabel("Horsepower"), Guide.ylabel("Acceleration"))
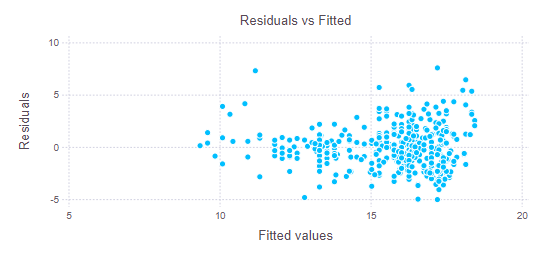
# 診断プロット1:Residuals vs Fitted
set_default_plot_size(16cm, 8cm)
res = dat[:Acceleration] - pred
Gadfly.plot(x = pred, y = res, Geom.point,
Guide.title("Residuals vs Fitted"),
Guide.xlabel("Fitted values"), Guide.ylabel("Residuals"))
# 診断プロット2:Normal Q-Q plot
set_default_plot_size(16cm, 16cm)
m = mean(res)
N = length(res)
stdRes = (res - m * ones(N)) / (std(res)) # 標準化誤差 = (誤差-平均)/標準偏差
qx = quantile.(Normal(), range(0.5, stop=(N-0.5), length=(N)) / (N + 1))
Gadfly.plot(layer(x = qx, y = sort(stdRes), Geom.point),
layer(x = [-3,3], y = [-3,3], Geom.line, style(line_style = [:dot])),
Guide.title("Normal Q-Q plot"),
Guide.xlabel("Theoretical Quantiles"),
Guide.ylabel("Standardized residuals"))
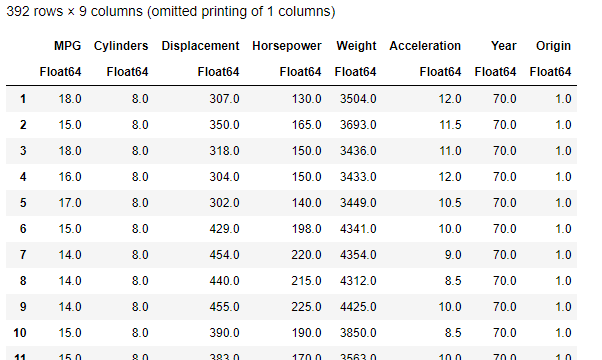
こんなデータです。いろいろプロットしてみます。
線形回帰してみますと。

残渣を見てみます。
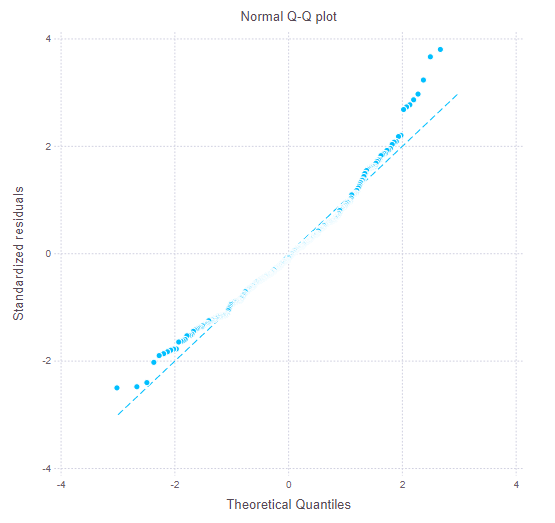
こちらのサイト「Julia でふつうの統計解析」を参考にさせていただきました。
