【R】正規性の検定

検定を行う前に、データが正規性を持つか（正規分布しているといえるか）を検証する必要があります。検証方法としては、コルモゴロフ・スミルノフ検定 (Kolmogorov-Smirnov test)やシャピロ・ウィルク検定 (Shapiro-Wilk test)があります。

コルモゴロフ・スミルノフ検定

コルモゴロフ・スミルノフ検定は得られた2つのデータ間の確率分布の相違の検定、または、1データにおける確率分布の正規性を行う検定。１データで正規分布に従うとみなせるか否かを有意水準5%にて検定してみます。帰無仮説 (H₀) は標本分布が正規分布に従うことです。

vx<-c(32, 38, 58, 51, 41, 55, 35, 66, 52, 54, 60, 66, 64, 43, 78, 51, 77, 81, 64, 46, 46, 29, 55, 31, 40, 72,41, 32, 66, 51, 83, 49, 32, 44, 49, 52)
hist(vx)
ks.test(x=vx,y="pnorm",mean=mean(vx),sd=sd(vx))

ヒストグラムで確認してみると、何となく正規分布しているようにも見えます。

検定結果が次のように表示されます。

	One-sample Kolmogorov-Smirnov test

data:  vx
D = 0.095672, p-value = 0.8967
alternative hypothesis: two-sided

この結果、p値が0.8967となっており、有意水準が5%でも対立仮設を棄却できず、帰無仮説が保留され、データvxは正規分布に従っているとみなすことができます。

シャピロ・ウィルク検定

シャピロ・ウィルク検定は、データが正規母集団に由来するという帰無仮説を検定します。帰無仮説 (H₀) は標本分布が正規分布に従うこととして、有意水準5%にて検定します。

vx<-c(57, 2, 67, 23, 50, 3, 52, 51, 48, 11, 51, 54, 44, 31, 54, 49, 22, 51, 11, 93, 58, 3, 51, 41, 91, 55, 35, 12, 66, 52, 54, 15)
hist(vx)
shapiro.test(x=vx)

ヒストグラムで分布を確認してみると、正規分布していないように見えます。

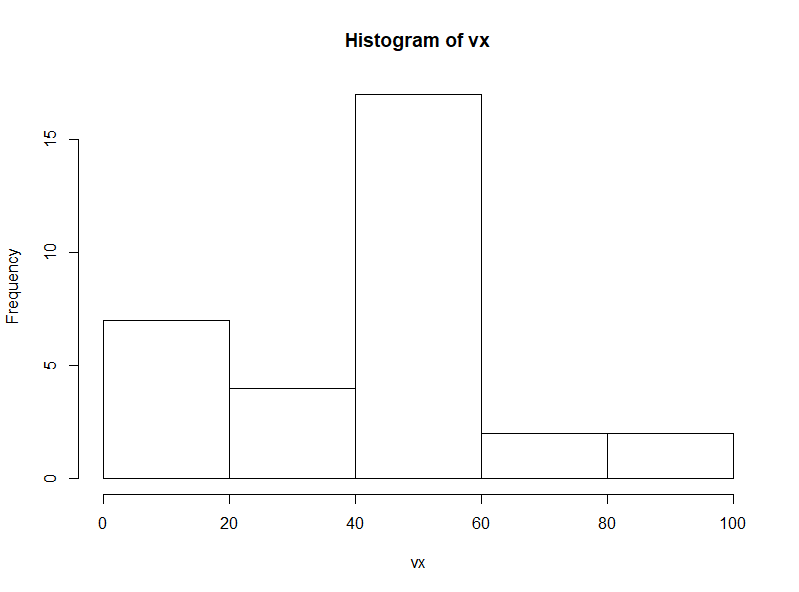
検定の結果は、次の通りになります。

	Shapiro-Wilk normality test

data:  vx
W = 0.92239, p-value = 0.02416

この検定では、p値が0.02416であるため、有意水準が5%で帰無仮説が棄却され 、データXの分布は正規分布に従うとはいえない と判断できます。