【R】ある事象のカイ二乗検定
2020年4月18日
ある事象がポアソン分布に従っているかどうかをカイ二乗検定にて確認します。統計検定2級2014年11月の問6の問題を解いてみます。
ある地域における1日の死亡者数の集計結果(500日間)の表があります。これがポアソン分布に従っているか調べます。
| 死亡者数(人) | 0 | 1 | 2 | 3 | 4 | 5 | 6人以上 | 計 |
| 件数(日数) | 55 | 144 | 140 | 95 | 45 | 15 | 9 | 500 |
dat<-data.frame("Died"=c(0, 1, 2, 3, 4, 5, 6), "Days"=c(55, 144, 140, 95, 45, 15, 6))
x<-dat$Died
mu<-dat$Died %*% dat$Days / 500
dat$E_Days<-sapply(x, function(x) {(ppois(x, mu)-ppois(x-1, mu))})
dat$E_Days[7]<-(1-ppois(5, mu))
dat
layout(matrix(1:2, 1, 2))
barplot(dat$Days, main="Days", names.arg = dat$Died)
barplot(dat$E_Days, main="E_Days",names.arg = dat$Died)
chisq.test(dat$Days,p=dat$E_Days)
死亡者数の平均値muを計算すると2.0でした(死亡者数が7人以上の日は、なかったとして)。
1日の死亡者数がポアソン分布に従っているか検定します。ポアソン分布は、以下であらわされます。
\(f(x)=\frac{e^{-\lambda} \lambda^x}{x!}\)
検定をするために、各死亡者数に対する期待度数を計算します。上式に、\(\lambda=2.0\)を入れて、各死亡者数xに対する期待度数を計算します。その結果が、下の表です。また、実測の度数と期待度数のヒストグラムは次の通りです。
| 死亡者数(人) | 0 | 1 | 2 | 3 | 4 | 5 | 6人以上 | 計 |
| 件数(日数) | 67.7 | 135.3 | 135.3 | 90.2 | 45.1 | 18.0 | 8.3 | 500 |
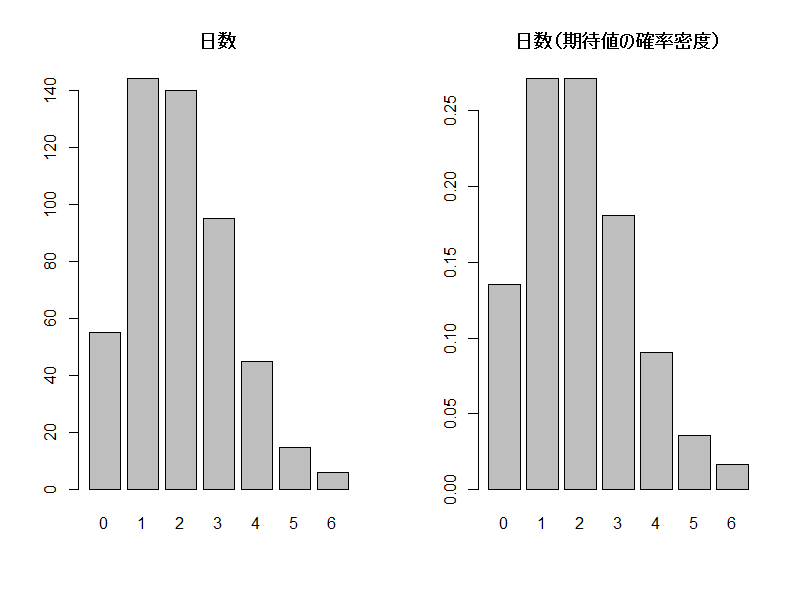
なんとなく似ていますね。実際の検定は、\(chisq.test()\)で行います。適合度の検定(goodness of fit test)になります。結果は次の通りです。R:
> chisq.test(dat$Days,dat$E_Days) Chi-squared test for given probabilities data: dat$Days X-squared = 4.4825, df = 6, p-value = 0.6117
帰無仮説を棄却できなかったため、この死亡者数はポアソン分布に従うといえます。
