【R】シンプソンのパラドックス

2020年4月26日

Simpson’s ParadoxをRで実践してみます。
ある3次元のデータ（X, Y, Z）があった時に、(X, Y)でデータの相関を見ると強い負の相関があったとしても、Zの情報をいれると、それが実は5つの群に分かれていて、それぞれの群を見ると強い正の相関であることがわかります。

次のコードで疑似的にデータを作成し、3つのプロットでそれを確認します。
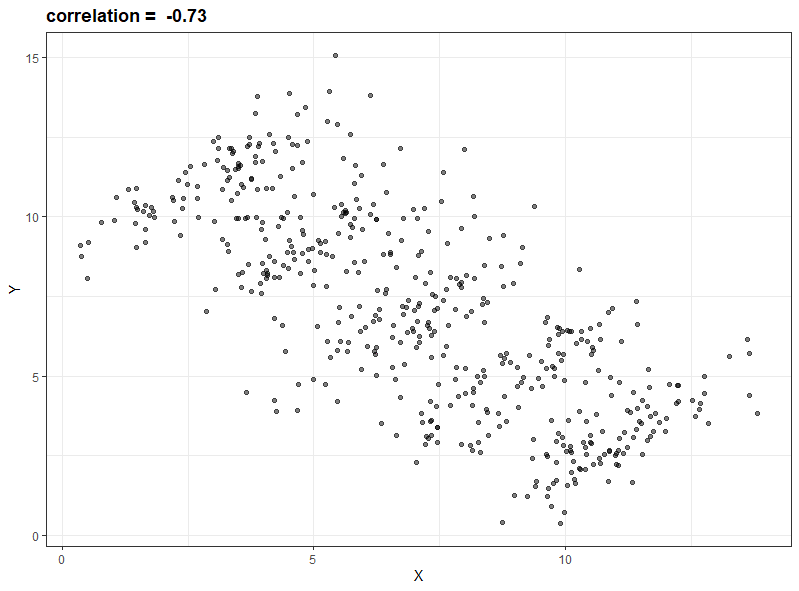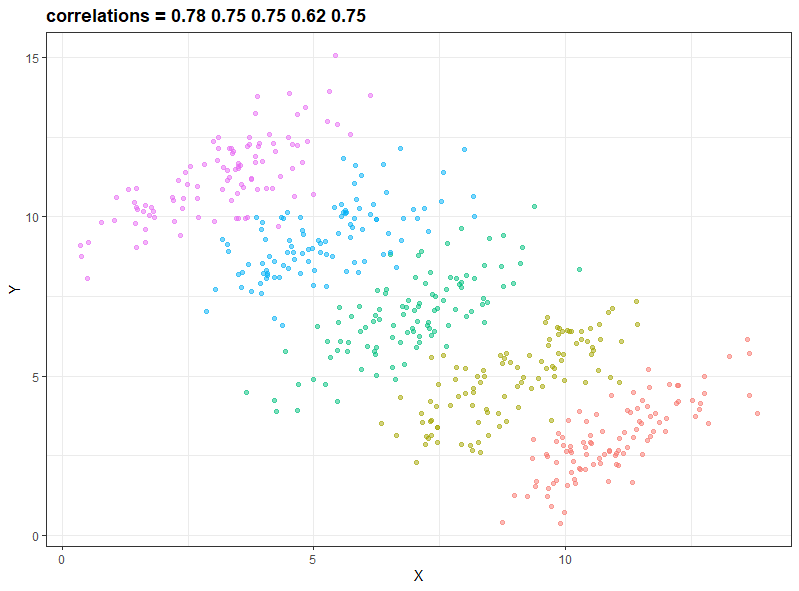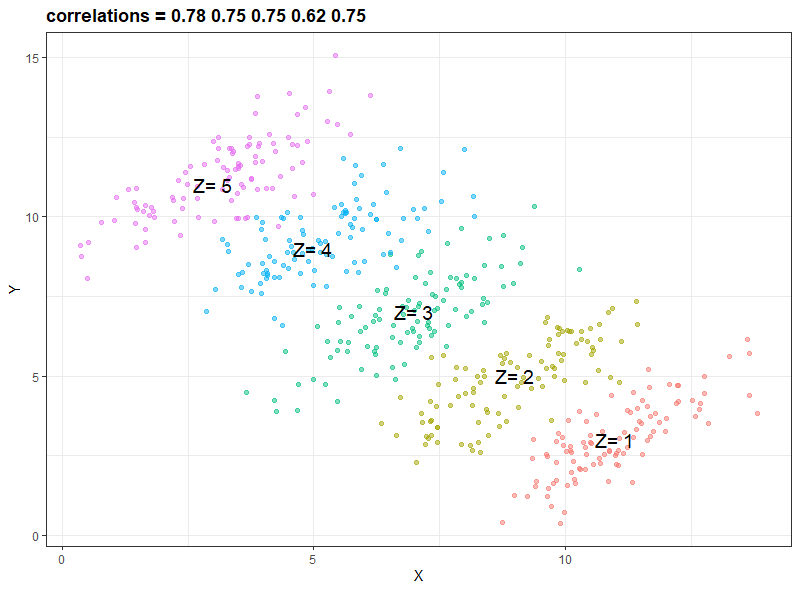
最初のプロットではZの情報はなく、X,Yの情報だけでX,Yの相関を見ています。この時、相関係数は-0.73と強い負の相関です。

次のプロットでは、Zの情報を入れて、それぞれの群を色分けします。各郡の相関係数を計算すると、それぞれ0.78, 0.75, 0.75, 0.62, 0.75と強い正の相関であることがわかります。

3番目のプロットでは各郡に名前を付けています。

3つのプロットをgifで出力し、Animated GIF makerにてアニメーションgifを作りました。

library(tidyverse)
library(dslabs)
ds_theme_set()

## simulate data 
N <- 100
Sigma <- matrix(c(1,0.75,0.75, 1), 2, 2)*1.5
means <- list(c(11,3), c(9,5), c(7,7), c(5,9), c(3,11))
dat <- lapply(means, function(mu) 
  MASS::mvrnorm(N, mu, Sigma))
dat<-as.data.frame(Reduce(rbind, dat)) %>%
  mutate(Z = as.character(rep(seq_along(means), each = N)))
names(dat) <- c("X", "Y", "Z")

## First plot
dat %>% ggplot(aes(X,Y)) + geom_point(alpha = .5) +
  ggtitle(paste("correlation = ", round(cor(dat$X, dat$Y), 2))) 

## second plot
means <- as.data.frame(Reduce(rbind, means)) %>% setNames(c("x","y")) %>%
  mutate(z = as.character(seq_along(means)))

corrs <- dat %>% group_by(Z) %>% summarize(cor = cor(X,Y)) %>% .$cor 

p <- dat %>% ggplot(aes(X, Y, color = Z)) + 
  geom_point(show.legend = FALSE, alpha = 0.5) +
  ggtitle(paste("correlations =",  paste(signif(corrs,2), collapse=" ")))
p

## third plot
p + annotate("text", x = means$x, y = means$y, 
             label = paste("Z=", means$z), cex = 5)