【R】判別分析
1.はじめに
判別分析(discriminant analysis)は、事前にあるグループに属するデータが与えられたときに、そのデータを元に学習し、次に与えられたデータがどのグループに属するか判断する基準(判別関数)を得る方法です。データは正規分布していることが前提です。
判別分析には、その判別関数の性質から次の種類がある。
・線形判別関数(LDA):平面・直線による判別。等分散性が必要(共分散行列を持つ)。
・二次判別関数(QDA):二次関数による判別。等分散性不要。
・非線形判別関数(MDA):超曲面・曲線などの非線形判別関数。
ここでは、簡単のため線形判別関数のみに注目する。データは、irisを用いる。
2.パッケージ
RのMASSパッケージを用いる。線形判別関数を用いるときは、lda関数を用いる。
3.データ準備
irisデータを学習用データ(train.data)とテストデータ(test.data)に分けます。irisデータは、Species毎に50個ずつあります。そのうち、各データの最初の455個を学習用に、残りの5個をテスト用に準備します。また、Speciesの名前が冗長なので、setosa、 versicolor、 virginica をそれぞれS、C、Vに置き換えます。
library(MASS)
train.data<-rbind(iris[c(1:45),], iris[c(51:95),], iris[c(101:145),])
test.data<-rbind(iris[c(46:50),], iris[c(96:100),], iris[c(146:150),])
train.data[,5]<-factor(c(rep("S",45),rep("C",45),rep("V",45)))
test.data[,5]<-factor(c(rep("S",5),rep("C",5),rep("V",5)))
4.判別関数
4.1 学習
学習用データを使って、lda関数で判別関数を求めます。グループは、Speciesです。これで、グループ分けします。
train.ret<-lda(Species~., train.data)
結果を見ますと次のようになります。
> train.ret
Call:
lda(Species ~ ., data = train.data)
Prior probabilities of groups:
C S V
0.3333333 0.3333333 0.3333333
Group means:
Sepal.Length Sepal.Width Petal.Length Petal.Width
C 5.964444 2.764444 4.293333 1.3355556
S 5.011111 3.431111 1.462222 0.2488889
V 6.617778 2.973333 5.593333 2.0222222
Coefficients of linear discriminants:
LD1 LD2
Sepal.Length -0.7931862 -0.1545859
Sepal.Width -1.4965526 2.2831061
Petal.Length 2.2284759 -0.6822534
Petal.Width 2.5967874 2.4834166
Proportion of trace:
LD1 LD2
0.9917 0.0083 求める判別関数は、変数と判別係数の線形結合となる。判別係数はLD1とLD2の2つが得られた。定数項は次で求められる。
> apply(train.ret$means %*% train.ret$scaling, 2, mean)
LD1 LD2
2.326653 6.475967 判別関数は、Sepal.Length、Sepal.Width、Petal.Length、Petal.Widthの変数をx_1, x_2, x_3, x_4として、次で表される。
-0.7931862 x_1 -1.4965526 x_2 + 2.2284759 x_3 + 2.5967874 x_4 + 2.326653 = 0
-0.1545859 x_1 + 2.2831061 x_2 -0.6822534 x_3 + 2.4834166 x_4 + 6.475967 = 0判別結果は、predict関数で得られる。predict()$class は判別されたグループのラベルで、どのグループに属するか示している。predict()$posterior は、どのグループに判別されているかの確率、predict()$xは、判別関数得点です。
> train.pdct<-predict(train.ret)
> train.pdct$class
[1] S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S C C C C C C C C C C C
[57] C C C C C C C C C V C C C C C C C C C C C C V C C C C C C C C C C C V V V V V V V V V V V V V V V V V V V V V V
[113] V V V V V V V V V V V C V V V V V V V V V V V
Levels: C S V
> train.pdct$posterior[c(1,47,102),]
C S V
1 8.616654e-22 1.000000e+00 3.214388e-41
52 9.991900e-01 4.600534e-19 8.100344e-04
112 3.034247e-03 2.202230e-36 9.969658e-01
> train.pdct$x[c(1,47,102),]
LD1 LD2
1 -7.970613 0.2680443
52 1.731310 0.4956068
112 5.301082 -0.1983824判別結果は、次のようにすると見やすくなります。
train.pdct<-predict(train.ret)
table(train.data[,5], train.pdct$class)
C S V
C 43 0 2
S 0 45 0
V 1 0 44この結果、Cは45個のうち2個正しく判別できず、Sは45個全て正しく判別でき、Vは1個正しく判別できなかったことになります。
ヒストグラムを表示してみます。
plot(train.ret, dimen=1)
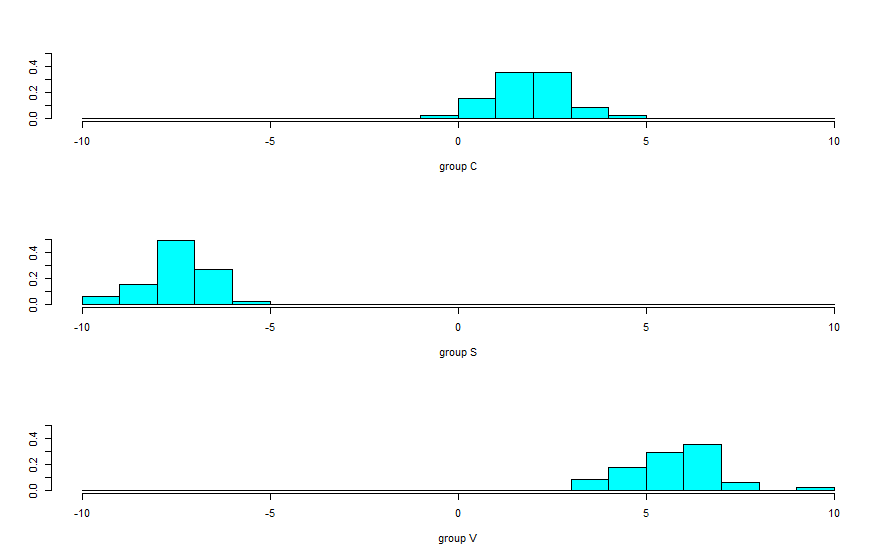
この結果からも、グループSは容易に正しく判別できそうです。
横軸に第一判別関数、縦軸に第二判別関数としたときの散布図は次のように描けます。
plot(train.ret, dimen=2)
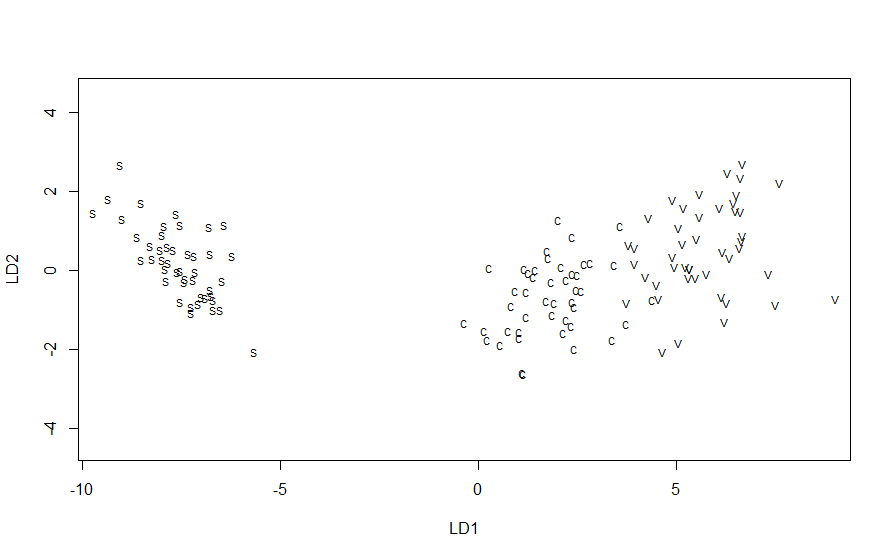
グループCとグループVは、それほど重なっていないことがわかります。
4.2 テスト
では、学習した判別関数を用いて、テストデータを判別してみましょう。
ret.test<-predict(ret, test.data) table(test.data[,5], test.ret$class)
C S V
C 5 0 0
S 0 5 0
V 0 0 5結果を見ますと、テストデータ5個を全て正しく判別できています。続いて、散布図で確認してみます。
plot(test.ret$x,type="n") text(test.ret$x,labels=test.data[,5])
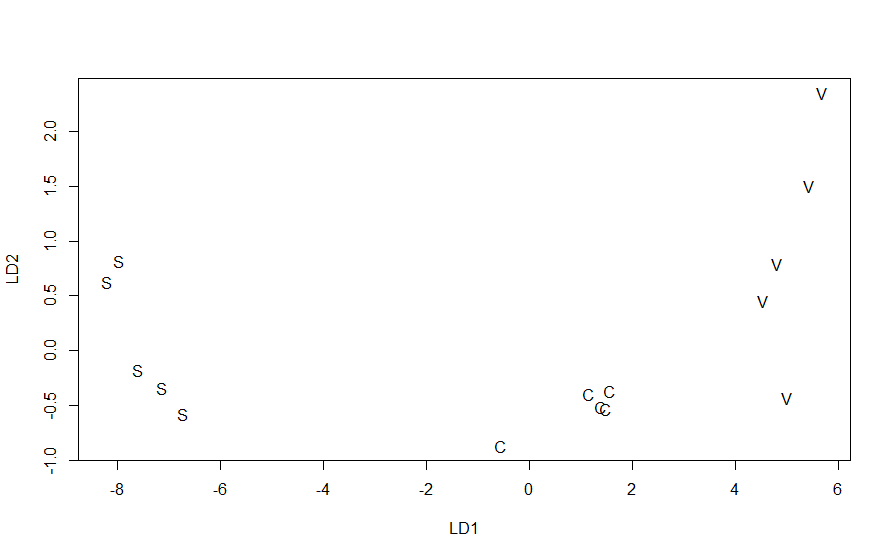
確かに、このデータですと、簡単に判別できそうですね。
5.さいごに
データを判別するためには良さそうですが、まず学習が必要です。また、今のところ、どの程度の精度で判別できるのか不明です。今後ももう少し調べてみたいです。
参考:
・Rと判別分析
・入門 統計学、栗原伸一、オーム社
・Rによる統計解析、青木繁伸、オーム社
