【R】線形回帰
1. はじめに
AIや機械学習が花盛りですが、究極の目標は、”予測”です。予測のためのツールの最も基本は(線形)回帰です。そこで、もう一回見てみます。
2. データ
データは、機械学習等のデータセットを含むmlbenchパッケージのデータセットBostonHousingを使います。
library(tidyverse) library(mlbench) data(BostonHousing)
> head(BostonHousing)
crim zn indus chas nox rm age dis rad tax ptratio b lstat medv
1 0.00632 18 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 396.90 4.98 24.0
2 0.02731 0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 396.90 9.14 21.6
3 0.02729 0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 392.83 4.03 34.7
4 0.03237 0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 394.63 2.94 33.4
5 0.06905 0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 396.90 5.33 36.2
6 0.02985 0 2.18 0 0.458 6.430 58.7 6.0622 3 222 18.7 394.12 5.21 28.73. 回帰
3. 1 モデル
住宅価格の中央値medvを目的変数として、それ以外を全て説明変数としてモデルを作ってみます。Rでは、lm関数で直線回帰のモデルを作ることができます。
model_full.lm <- lm(medv ~ crim + zn + indus + chas + nox + rm + age + dis + rad + tax + ptratio + b + lstat, data=BostonHousing)
要約を見てみます。
summary(model_full.lm)
> summary(model_full.lm)
Call:
lm(formula = medv ~ crim + zn + indus + chas + nox + rm + age +
dis + rad + tax + ptratio + b + lstat, data = BostonHousing)
Residuals:
Min 1Q Median 3Q Max
-15.595 -2.730 -0.518 1.777 26.199
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.646e+01 5.103e+00 7.144 3.28e-12 ***
crim -1.080e-01 3.286e-02 -3.287 0.001087 **
zn 4.642e-02 1.373e-02 3.382 0.000778 ***
indus 2.056e-02 6.150e-02 0.334 0.738288
chas1 2.687e+00 8.616e-01 3.118 0.001925 **
nox -1.777e+01 3.820e+00 -4.651 4.25e-06 ***
rm 3.810e+00 4.179e-01 9.116 < 2e-16 ***
age 6.922e-04 1.321e-02 0.052 0.958229
dis -1.476e+00 1.995e-01 -7.398 6.01e-13 ***
rad 3.060e-01 6.635e-02 4.613 5.07e-06 ***
tax -1.233e-02 3.760e-03 -3.280 0.001112 **
ptratio -9.527e-01 1.308e-01 -7.283 1.31e-12 ***
b 9.312e-03 2.686e-03 3.467 0.000573 ***
lstat -5.248e-01 5.072e-02 -10.347 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.745 on 492 degrees of freedom
Multiple R-squared: 0.7406, Adjusted R-squared: 0.7338
F-statistic: 108.1 on 13 and 492 DF, p-value: < 2.2e-16Summary関数で、RSE(Residual Standard Error)も表示されます。モデルの評価で重要な性能指標は、平均二乗誤差平方根(RMSE: Root mean square error)です。これは、適合率の指標であり他モデルと比較する基準となります。ここでは、分母がレコード数ではなく自由度とするRMEが表示されます。レコード数が少ない場合はこちらの方が良いのですが、多い場合にはその差はあまりありません。
この結果を見ると、indusとageはほとんど寄与していないようですので、これらの説明変数を除いて再度モデルを作ってみます。
model_optm.lm <- lm(medv ~ crim + zn + chas + nox + rm + dis + rad + tax + ptratio + b + lstat, data=BostonHousing) summary(model_optm.lm)
> summary(model_optm.lm)
Call:
lm(formula = medv ~ crim + zn + chas + nox + rm + dis + rad +
tax + ptratio + b + lstat, data = BostonHousing)
Residuals:
Min 1Q Median 3Q Max
-15.5984 -2.7386 -0.5046 1.7273 26.2373
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 36.341145 5.067492 7.171 2.73e-12 ***
crim -0.108413 0.032779 -3.307 0.001010 **
zn 0.045845 0.013523 3.390 0.000754 ***
chas1 2.718716 0.854240 3.183 0.001551 **
nox -17.376023 3.535243 -4.915 1.21e-06 ***
rm 3.801579 0.406316 9.356 < 2e-16 ***
dis -1.492711 0.185731 -8.037 6.84e-15 ***
rad 0.299608 0.063402 4.726 3.00e-06 ***
tax -0.011778 0.003372 -3.493 0.000521 ***
ptratio -0.946525 0.129066 -7.334 9.24e-13 ***
b 0.009291 0.002674 3.475 0.000557 ***
lstat -0.522553 0.047424 -11.019 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.736 on 494 degrees of freedom
Multiple R-squared: 0.7406, Adjusted R-squared: 0.7348
F-statistic: 128.2 on 11 and 494 DF, p-value: < 2.2e-16
Adjusted R-squaredの値を見るとほとんど変わっていません。説明変数は少ないほうが良いので、このままmodel_optm.lmを使うことにします。
indusとageの説明変数を減らすことは、赤池情報量基(AIC)からも明白です。MASSパッケージを使うとこのことを簡単に調べられます。stepAICという関数で段階的回帰を行い、最適な説明変数を選択できます。
library(MASS) step <- stepAIC(model_full.lm, direction="both")
これを実行すると段階的にAICを計算しながら減らせる変数を選んでくれます。
Step: AIC=1585.76
medv ~ crim + zn + chas + nox + rm + dis + rad + tax + ptratio +
b + lstat
Df Sum of Sq RSS AIC
<none> 11081 1585.8
+ indus 1 2.52 11079 1587.7
+ age 1 0.06 11081 1587.8
- chas 1 227.21 11309 1594.0
- crim 1 245.37 11327 1594.8
- zn 1 257.82 11339 1595.4
- b 1 270.82 11352 1596.0
- tax 1 273.62 11355 1596.1
- rad 1 500.92 11582 1606.1
- nox 1 541.91 11623 1607.9
- ptratio 1 1206.45 12288 1636.0
- dis 1 1448.94 12530 1645.9
- rm 1 1963.66 13045 1666.3
- lstat 1 2723.48 13805 1695.03. 2 予測
Rでは、次のように予測ができます。
model_full.fit <- predict(model_optm.lm)
また、残差は以下で求められます。
model.redid <- residuals(v.lm)
3.3 診断
診断は、結果をプロットしてみることが多いです。Rでは、plot()関数で簡単にプロットしてくれます。また、ggplotを使うとより高度な表現ができます。
診断に関しては”Residuals and Diagnostics For linear regression Using R”のサイトが役に立ちます。
3.3.1 QQプロット
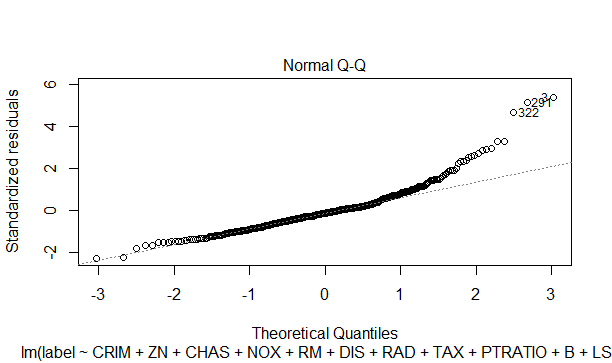
QQプロットは、実測値と予測値がどの程度同じ分布をしているかを示すプロットです。正規化された残差を低いものから高いものに並べます。値をy軸に、それに対応する標準正規分布の累積分布関数をx軸にします。プロットがほぼ対角線上にあるなら実測値と予測値の分布は近いことになります。誤差データが正規分布しているかを確認できます。
plot(model_optm.lm,which = 2)
3.3.2 予測値に対する残差のプロット
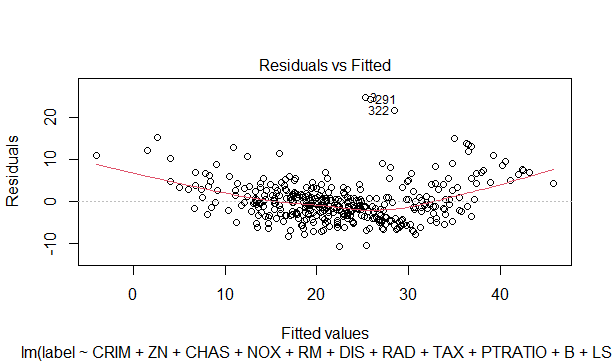
予測値x軸に対して、どれだけ残差があるかをy軸に示します。理想的にはfitしたモデルに対して残差は0を中心に一様に分布します。変な曲線ですと直線でのfitが良くない可能性があります。
plot(model_optm.lm,which = 1)
3.3.3 正規化した残差の絶対値の平方根のプロット
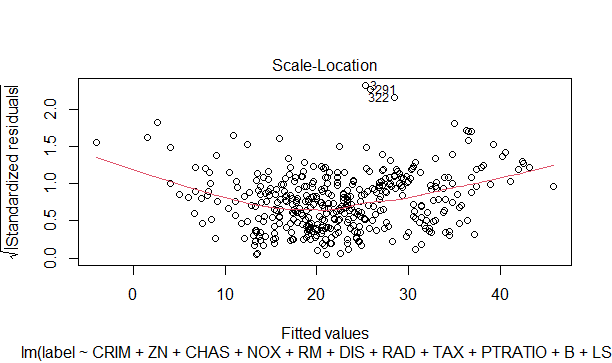
残差のバラつき状況を確認できます。予測値をx軸に、正規化した残差の絶対値の平方根をy軸にとります。一様に分布していると、ほぼ一定の値となります。値が増加/減少傾向だと等分散性が疑われます。
plot(model_optm.lm,which = 3)
3.3.4 Leverageに対する標準化した残差のプロット
予測値が大きく外れているかどうかを確認できます。クック距離を基準として、0.5だと影響大、1だと大きく外れているとみなされます。クック距離は、プロットに点線で表示されます。
plot(model_optm.lm,which = 5)
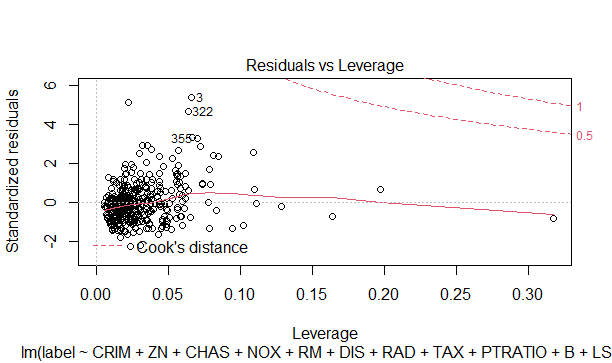
上記、4つのデータは、以下のようにすると一度に表示してくれます。
par(mfrow = c(2, 2)) plot(model_optm.lm)
また、ggfortifyというパッケージでもきれいに描いてくれます。
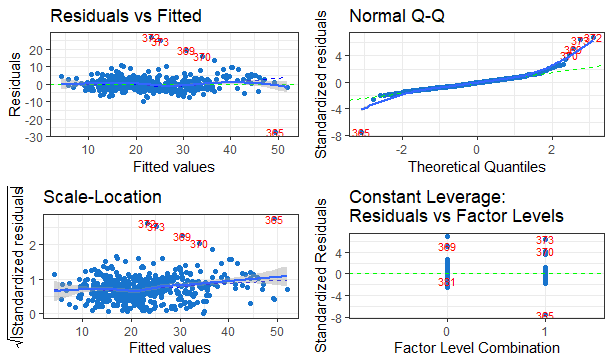
library(ggfortify) autoplot(model_optm.lm)
このggfortifyは、ggplotに準拠しているので、自由にカスタイマイズできます。
autoplot(model.lm, colour = 'dodgerblue3',
smooth.colour = 'blue', smooth.linetype = 'dashed',
ad.colour = 'green',
label.size = 3, label.n = 5, label.colour = 'red') + theme_bw() + geom_smooth()
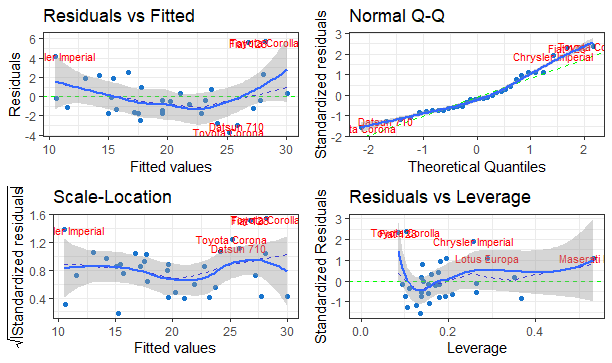
4. モデルの改良
今までは、線形回帰モデルのみ見てきました。基本的に線形回帰で満足できる結果が得られればそれで充分です。しかし、回帰に直線ではなく多項式等を利用するとよりよくデータにフィットする場合があります。その時は、多項式回帰等を利用すると良いです。
4. 1 多項式回帰
多項式回帰は、モデルでploy()関数を利用します。コンマで区切り次数を指定できます。あらかじめ、どの多項式が良いか確認しておきます。
例えば、crimとmedvの関係を見てみると。
BostonHousing %>% ggplot(aes(crim, medv))+ geom_point()+ geom_smooth()
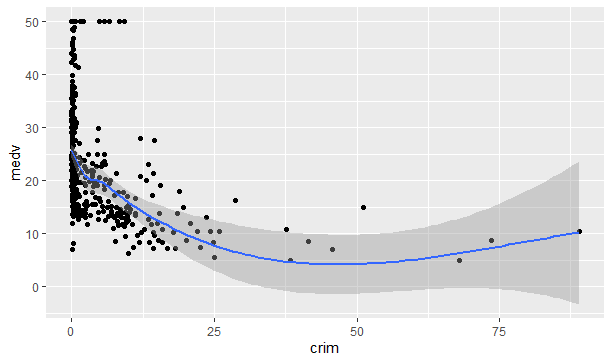
もしかしたら、2次関数が良いかもしれません。同様に他の説明変数と目的変数の関係を確認して、radは3次、rmは2次、lstatは2次ということがわかりました。そこで、次のようにモデル化します。
model_optm2.lm <- lm(medv ~ poly(crim,2) + zn + chas + nox + poly(rm,2) + dis + poly(rad,3) + tax + ptratio + b + poly(lstat,2), data=BostonHousing) summary(model_optm2.lm)
Call:
lm(formula = medv ~ poly(crim, 2) + zn + chas + nox + poly(rm,
2) + dis + poly(rad, 3) + tax + ptratio + b + poly(lstat,
2), data = BostonHousing)
Residuals:
Min 1Q Median 3Q Max
-27.4387 -2.3635 -0.1795 1.7757 26.6794
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 49.216373 3.344861 14.714 < 2e-16 ***
poly(crim, 2)1 -39.093403 6.903006 -5.663 2.54e-08 ***
poly(crim, 2)2 14.419352 6.218406 2.319 0.02082 *
zn 0.021946 0.011772 1.864 0.06289 .
chas1 2.365309 0.715458 3.306 0.00102 **
nox -14.895100 2.977260 -5.003 7.89e-07 ***
poly(rm, 2)1 55.324341 5.539381 9.987 < 2e-16 ***
poly(rm, 2)2 43.053622 4.627378 9.304 < 2e-16 ***
dis -1.170616 0.159179 -7.354 8.16e-13 ***
poly(rad, 3)1 61.374714 11.929651 5.145 3.89e-07 ***
poly(rad, 3)2 0.208399 4.228171 0.049 0.96071
poly(rad, 3)3 8.849151 4.179466 2.117 0.03474 *
tax -0.009371 0.002852 -3.286 0.00109 **
ptratio -0.693132 0.111097 -6.239 9.55e-10 ***
b 0.006240 0.002265 2.755 0.00609 **
poly(lstat, 2)1 -93.300097 6.619431 -14.095 < 2e-16 ***
poly(lstat, 2)2 32.626160 4.909401 6.646 8.07e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.956 on 489 degrees of freedom
Multiple R-squared: 0.8208, Adjusted R-squared: 0.815
F-statistic: 140 on 16 and 489 DF, p-value: < 2.2e-16
この結果、Adjusted R-squaredが0.815と飛躍的に向上していることが分かります。
autoplot(model_optm2.lm, colour = 'dodgerblue3',
smooth.colour = 'blue', smooth.linetype = 'dashed',
ad.colour = 'green',
label.size = 3, label.n = 5, label.colour = 'red') + theme_bw() + geom_smooth()